不要错过PHP和阿姆斯特朗数的爱恨情仇
时间:2022-02-11 13:34
各位看客,疑问有没有充满你大大的脑袋?哈哈,别懵,今天又要给大家介绍一个好玩的方法,翻译本文标题的大白话就是“用PHP检查一个数是否是阿姆斯特朗数”,阿姆斯特朗数其实也就是水仙花数,那这到底啥数才是水仙花?又怎么用PHP程序实现?下面我们就来一一介绍~
首先给大家介绍水仙花数即阿姆斯特朗数的定义:
水仙花数也被称为超完全数字不变数、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number)。水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身(例如:1^3 + 5^3+ 3^3 = 153)。
这下应该明白了吧,然后咱们继续:
直接打开编辑器,上代码!
<?php
function armstrong_number($num) {
$sl = strlen($num);
$sum = 0;
$num = (string)$num;
for ($i = 0; $i < $sl; $i++) {
$sum = $sum + pow((string)$num{$i},$sl);
}
if ((string)$sum == (string)$num) {
return "True";
} else {
return "False";
}
}
echo "153是阿姆斯特朗数吗?".armstrong_number(153);
echo "<br>21是阿姆斯特朗数吗?".armstrong_number(21);
echo "<br>4587是阿姆斯特朗数吗?".armstrong_number(4587);来运行结果看看:
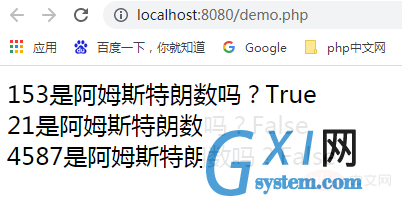
上述例子里,我们给了三个数进行判断,分别是153、21、4587。
明显153是阿姆斯特朗数,而21和4587都不是,所以返回了false。
其实在PHP程序中想要实现判断是不是阿姆斯特朗数,最关键的一点就是它的判定公式!
正如上面定义所说的,符合每个位上的数字的3次幂之和等于它本身的数就称之为阿姆斯特朗数,也就是水仙花数。
那么示例中一个关键代码部分就是“$sum =$sum + pow((string)$num{$i},$sl);”了。
这里pow()是PHP中一个内置函数,用于计算x的y次方。
至此,是不是就浅显易懂了?
虽然不难,但是个人觉得比较有意思,这样的思路,也希望能帮助到需要的朋友~
PHP视频教程请戳->https://www.gxlsystem.com/course/list/29/type/2.html
以上就是不要错过PHP和阿姆斯特朗数的爱恨情仇的详细内容,更多请关注gxlsystem其它相关文章!