Python二叉树怎么实现

时间：2023-05-03 09:32

Python实现二叉树

Python二叉树怎么实现

Python实现二叉树可以使用面向对象编程的方式，通过定义二叉树节点类来实现。每个节点包含一个数据元素、左右子节点指针和一些操作方法，如插入节点、查找节点、删除节点等。

以下是一个简单的二叉树实现示例：

class Node:    def __init__(self, data):        self.data = data        self.left = None        self.right = None    def insert(self, data):        if self.data:            if data < self.data:                if self.left is None:                    self.left = Node(data)                else:                    self.left.insert(data)            elif data > self.data:                if self.right is None:                    self.right = Node(data)                else:                    self.right.insert(data)        else:            self.data = data    def find(self, data):        if data < self.data:            if self.left is None:                return str(data) + " Not Found"            return self.left.find(data)        elif data > self.data:            if self.right is None:                return str(data) + " Not Found"            return self.right.find(data)        else:            return str(self.data) + " is found"    def inorder_traversal(self, root):        res = []        if root:            res = self.inorder_traversal(root.left)            res.append(root.data)            res = res + self.inorder_traversal(root.right)        return res

在上述代码中，Node类定义了一个节点，包含数据元素data，以及左右子节点指针left和right。insert方法用于向二叉树中插入节点，find方法用于查找二叉树中是否存在特定节点，inorder_traversal方法用于对二叉树进行中序遍历。

下面是如何使用这个Node类来创建一个二叉树：

root = Node(50)root.insert(30)root.insert(20)root.insert(40)root.insert(70)root.insert(60)root.insert(80)# 查找节点print(root.find(70)) # Output: 70 is foundprint(root.find(90)) # Output: 90 Not Found# 中序遍历print(root.inorder_traversal(root)) # Output: [20, 30, 40, 50, 60, 70, 80]

在上述代码中，首先创建了一个根节点root，然后使用insert方法向树中插入节点，最后使用find方法查找节点并使用inorder_traversal方法对二叉树进行中序遍历。

除了插入、查找和遍历方法，二叉树还有其他的操作方法，如删除节点、判断是否为二叉搜索树、计算树的深度等。下面是一个稍微完整一些的二叉树示例代码：

class Node:    def __init__(self, data):        self.data = data        self.left = None        self.right = None    def insert(self, data):        if self.data:            if data < self.data:                if self.left is None:                    self.left = Node(data)                else:                    self.left.insert(data)            elif data > self.data:                if self.right is None:                    self.right = Node(data)                else:                    self.right.insert(data)        else:            self.data = data    def find(self, data):        if data < self.data:            if self.left is None:                return None            return self.left.find(data)        elif data > self.data:            if self.right is None:                return None            return self.right.find(data)        else:            return self    def delete(self, data):        if self is None:            return self        if data < self.data:            self.left = self.left.delete(data)        elif data > self.data:            self.right = self.right.delete(data)        else:            if self.left is None:                temp = self.right                self = None                return temp            elif self.right is None:                temp = self.left                self = None                return temp            temp = self.right.minimum()            self.data = temp.data            self.right = self.right.delete(temp.data)        return self    def minimum(self):        if self.left is None:            return self        return self.left.minimum()    def is_bst(self):        if self.left:            if self.left.data > self.data or not self.left.is_bst():                return False        if self.right:            if self.right.data < self.data or not self.right.is_bst():                return False        return True    def height(self, node):        if node is None:            return 0        left_height = self.height(node.left)        right_height = self.height(node.right)        return max(left_height, right_height) + 1    def inorder_traversal(self, root):        res = []        if root:            res = self.inorder_traversal(root.left)            res.append(root.data)            res = res + self.inorder_traversal(root.right)        return res

在这个示例中，我们新增了delete方法来删除指定的节点；minimum方法来查找树中的最小节点；is_bst方法来判断当前树是否为二叉搜索树；height方法来计算树的深度。

我们可以用以下代码来测试新增的方法：

# 创建二叉树root = Node(50)root.insert(30)root.insert(20)root.insert(40)root.insert(70)root.insert(60)root.insert(80)# 删除节点print("Deleting node 20:")root.delete(20)print(root.inorder_traversal(root))# 判断是否为二叉搜索树print("Is it a BST?:", root.is_bst())# 计算树的深度print("Tree height:", root.height(root))

这样我们就完成了一个比较完整的二叉树的实现，同时也演示了如何在Python中使用面向对象编程思想来实现一个数据结构。

最后附上完整的二叉树类实现代码：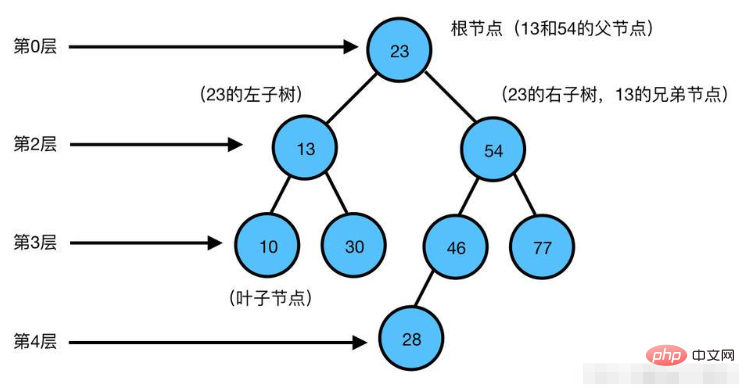

class Node:    def __init__(self, data):        self.data = data        self.left = None        self.right = None    def insert(self, data):        if self.data:            if data < self.data:                if self.left is None:                    self.left = Node(data)                else:                    self.left.insert(data)            elif data > self.data:                if self.right is None:                    self.right = Node(data)                else:                    self.right.insert(data)        else:            self.data = data    def find(self, data):        if data < self.data:            if self.left is None:                return None            return self.left.find(data)        elif data > self.data:            if self.right is None:                return None            return self.right.find(data)        else:            return self    def delete(self, data):        if self is None:            return self        if data < self.data:            self.left = self.left.delete(data)        elif data > self.data:            self.right = self.right.delete(data)        else:            if self.left is None:                temp = self.right                self = None                return temp            elif self.right is None:                temp = self.left                self = None                return temp            temp = self.right.minimum()            self.data = temp.data            self.right = self.right.delete(temp.data)        return self    def minimum(self):        if self.left is None:            return self        return self.left.minimum()    def is_bst(self):        if self.left:            if self.left.data > self.data or not self.left.is_bst():                return False        if self.right:            if self.right.data < self.data or not self.right.is_bst():                return False        return True    def height(self, node):        if node is None:            return 0        left_height = self.height(node.left)        right_height = self.height(node.right)        return max(left_height, right_height) + 1    def inorder_traversal(self, root):        res = []        if root:            res = self.inorder_traversal(root.left)            res.append(root.data)            res = res + self.inorder_traversal(root.right)        return resif __name__ == '__main__':    # 创建二叉树    root = Node(50)    root.insert(30)    root.insert(20)    root.insert(40)    root.insert(70)    root.insert(60)    root.insert(80)    # 删除节点    print("Deleting node 20:")    root.delete(20)    print(root.inorder_traversal(root))    # 判断是否为二叉搜索树    print("Is it a BST?:", root.is_bst())    # 计算树的深度    print("Tree height:", root.height(root))

运行代码后，可以得到以下输出：